TL;DR We study the algorithm used by Mekotio (also known as BestaFera), a banking Trojan that started targeting Brazilian users and now targets Spanish and LATAM users, to decrypt the strings contained within the program file. This post is motivated by a current publication of the Spanish National Institute of Cybersecurity (INCIBE), in which they analyze a sample of this family in detail. See the full report here. We first reverse-engineer the algorithm and then implement a solution in Python to brute-force the decryption key. Here we go!
Introduction
Mekotio is an advanced banking Trojan malware that incorporates interesting features, such as clipboard hijacking to steal money from bitcoin wallets. In addition, it watches the user activity in common web browsers (Firefox, Edge, and Opera, among others), overlaying HTML in the browser window of the bank website to steal the user’s credentials. It also relies on AutoHotKey to evade detection and make the analysis harder. You can read more details on this malware family here, here, and here.
In this post, we have considered the malware sample with the SHA-256 hash:
9572a6e0d50bd67c35cb70653661719c6c8034254f55e4693cfbfafb2768c59cwhich is a PE32+ DLL. This file needs to be loaded with the AutoHotKey interpreter and an AutoHotKey script. More details in the content of this script can be read in the full report of INCIBE (basically, the script loads a small 32/64-bit assembly code into the memory to dynamically resolve certain Windows APIs and change the permissions of the allocated memory with PAGE_EXECUTE_READWRITE to enable later execution).
The algorithm
If you check for the strings in the file, you will rapidly see that there are very few “normal” strings. If you look closer, you will find out that there are A LOT of strings codified in hexadecimal:
$ strings 9572a6e0d50bd67c35cb70653661719c6c8034254f55e4693cfbfafb2768c59c | grep -E "^[0-9A-F]*$"
56789
34934
FDA9
FDD9
C0A9
67889C4D8B88D91FD1769A3337D9133E
71F1022AC15088A791B866E1
EE669E47E11149EA5D8CBB1B
7CF03237D263EC072AC276F53EE61BC667E3
92DD15C67EB228D87EA14587F120D4B24691A73FFF5CC7CCAF
[ ... redacted ... ]
96DC1AC178B92FF21C35C1182DDA0B38F5648BD560FA24B174DD06303B83A52FD2053DAA448F528AC9718C963AFD30D57DA929B0A04BF9097AA15288A7E619C877A5509D429545BB69E11EB74A
589D46F4120D45
81E11CC06399CC72A04F8BD1163F
19BA66D5042AAA
1F6EBC51F439AA74F6
45B467ED12DE7C8EB66BA4D1
33BA48F62DD87FAB988B4388AA
8ACC6EDD1CC203
8ACC6EDD1CC203
[ ... redacted ... ]
33333
3333
3333
33333
333333
3333333
333333333333333333As introduced in the report of INCIBE, the algorithm that decrypts the strings is the function located at 0x94E2D0. The explanation given in the report about this function is a little… cryptic (yeah, that’s a good adjective). So, let us explain it again. (First things first! To be able to reverse engineer the function, we need to fully understand it!).
We will use the Ghidra tool to disassemble it. The first basic block of this function is this one:
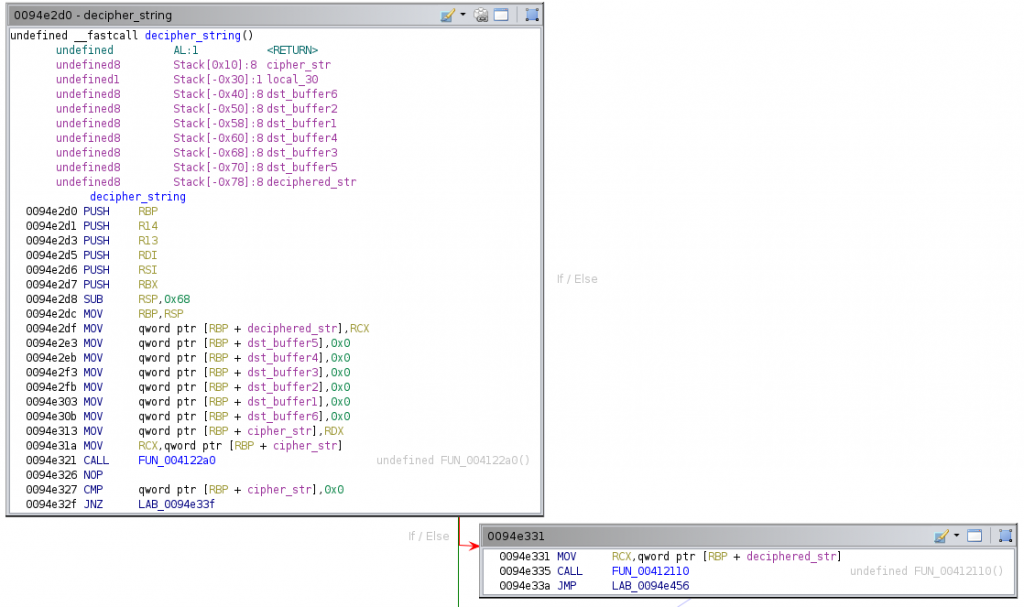
As shown, the function defines 9 local variables and receives two parameters, which are stored in [rbp + 0x78] and [rbp + 0x10] (passed on the rcx and rdx registers, respectively). These parameters are indeed pointers to strings. Recall that the calling convention on x64 follows the Microsoft ABI: the first four integer (or pointer parameters) are passed in the rcx, rdx, r8, and r9 registers, while additional arguments are passed on the stack. After the initialization of these variables to zero, it checks if the cipher string is null. If so, it will finish the function. Otherwise, the decryption algorithm begins:
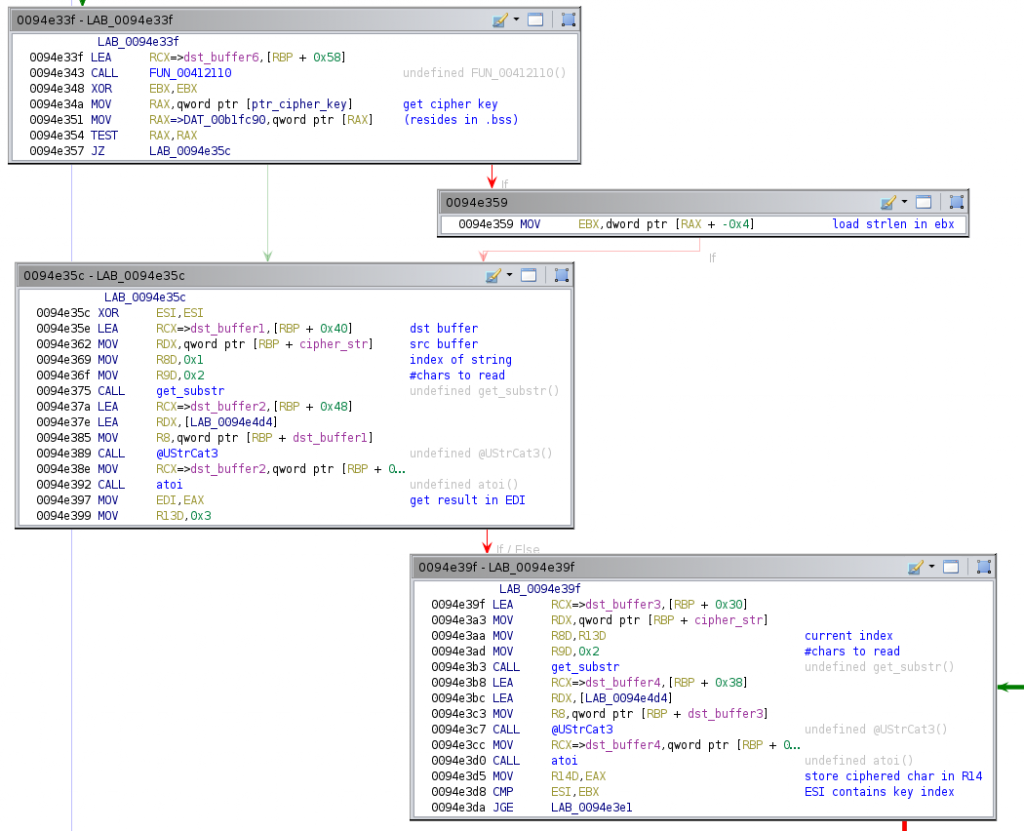
After clearing the content of [rbp + 0x58], it sets a zero in the ebx register and loads in rax the pointer to the decryption key. In case it is not zero, it sets in ebx the length of the decryption key (after studying this, we came to the conclusion that a string pointer contains in its previous byte its length). The block 0x94e35c then begins, clearing the esi register and loading in dst_buffer1 the first two chars of the cipher string. Recall that the strings are encoded in hexadecimal, and thus every two chars represents in fact one byte. These two chars are moved to another local buffer to finally convert them to from the ASCII representation to their corresponding integer value. The result is finally stored in the edi register (recall that by the calling convention, eax contains the return value of the function). This block ends storing in r13 a value of 3. This register will be used as an index for the deciphering loop, as you will see now.
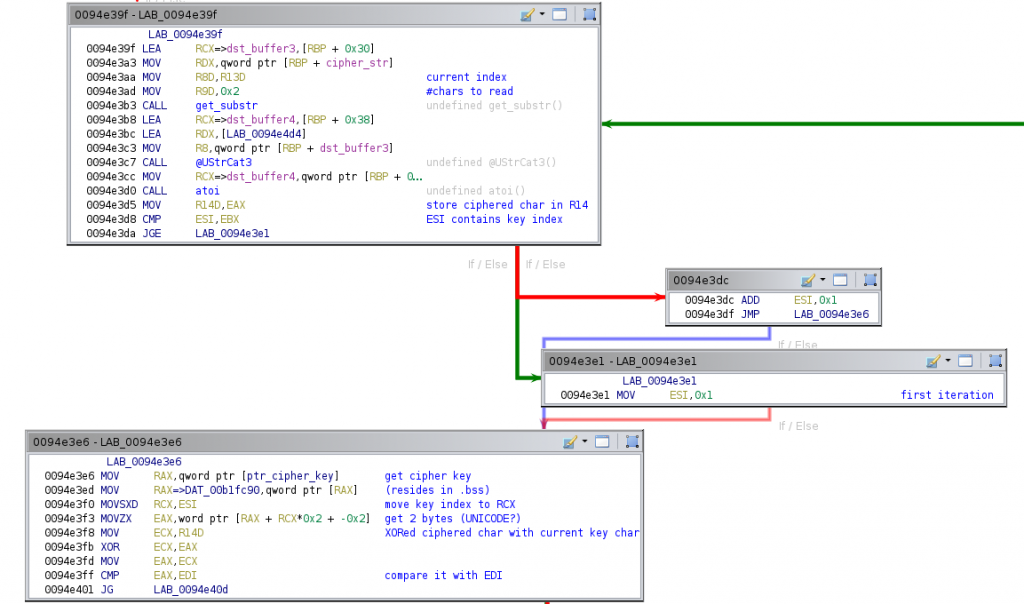
The block 0x94e35c that we have explained is the loop header block. The loop body starts in the 0x94e39f. The first instructions of this block perform a similar behavior as the loop header: it gets two chars of the cipher string, indicated by r13, moves them to a temporal buffer, and converts them to ther corresponding integer value. The result in this case is moved to the r14 register. Finally, it checks if esi (cleared in the loop header block, hence in the first iteration its value is zero) is greater than or equal to ebx (which contains the length of the decryption key, read again the previous paragraph!). If so, it resets the value of esi to one (block 0x94e3e1). Otherwise, it increments the value of esi in one unit (block 0x94e3dc). This register is being used to index the cipher key, as you will see now.
The next block (0x94e3e6) performs the decryption. It gets the pointer of the decryption key and, through indirect access, gets the two bytes pointed by the rcx register (which is previously loaded with esi) and stores them in eax, zeroing the upper 16 bits of the register. It then gets the value of r14 in ecx and XORes it with eax. The result is then moved to eax again and then compared with the edi register. The latter register was previously set to the integer representation of the first two bytes of the cipher string (see explanation of the previous block 0x94e35c). A weird thing is that it is getting two bytes from the decryption key, while only one byte was considered from the cipher string. We guess the decryption key must be UNICODE encoded, and thus there is a null byte after every byte with content which does not affect the XOR operation. This block ends comparing eax with edi.
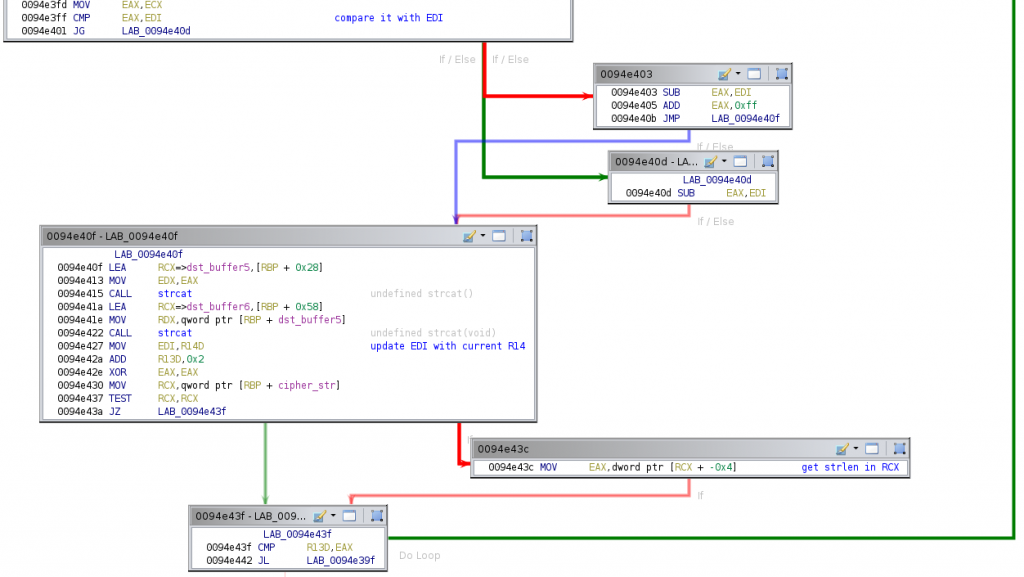
It then subtracts edi to eax, and adds to eax the value 0xff when eax is greater than edi , which guarantees a positive value in eax after the subtraction. Then, the final block of the loop begins. The result is first stored in a temporal buffer and then concatenated to dst_buffer6, which will contain the decrypted string within the loop. Finally, edi is updated with the value of r14 and r13 (the index used to access the cipher string in the first block of the loop body) is incremented by two units. This block ends checking whether the cipher string has been fully processed. When some chars are still unprocessed, the loop body starts again. Otherwise, the last two blocks of the function are executed.
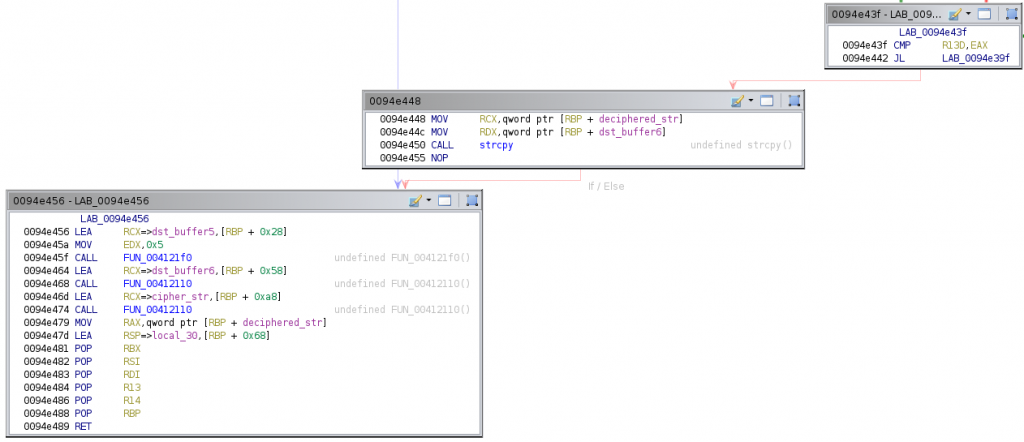
The dst_buffer6 is copied to [rbp + 0x78], which is then returned in rax to the caller. And that’s all from the function used by this sample of Mekotio to decrypt strings!
A Python implementation to brute-force the decryption key
Ok, now let’s try to brute-force the decryption key. We know how the algorithm works and have seen that it is similar to a decryption algorithm with feedback, as in each step the value of edi is updated, which is used in the next iteration for checking the positivity of the subtraction operation performed after the block 0x94e3e6.
We can build a quick-and-dirty function in Python to brute-force the decryption key. As input, the function will accept two parameters: the cipher string and the deciphered string. As output, it will return a list containing the bytes that conform the decryption key. An implementation of this function can be as follows:
def bruteforce_key(enc_str: str, dec_str: str) -> list:
idx = 0
# first iteration
edi = int(enc_str[idx:idx + 2], base= 16) # convert to int
key_list = []
dec_idx = 0
guess_key = 0
while guess_key < 256:
var2 = int(enc_str[idx + 2:idx + 4], base= 16) # convert to int
xor_val = guess_key ^ var2 # xored it
sub = xor_val - edi
if (sub < 0): # check if negative
sub += 0xff
if (sub == ord(dec_str[dec_idx])): # match?
key_list.append(guess_key)
dec_idx += 1
edi = var2
idx += 2
guess_key = 0 # reset for the next byte of guess key
else:
guess_key += 1 # try next key
if dec_idx == len(dec_str):
return key_listNow we can use one of the (long) strings given in the report of INCIBE of this sample to get the decryption key. Let’s try it:
ciphered_str = "48A543EE1E1C081EC87298CA6E984D2BF2592ABF62F51240FA2DC7659A39094BF224DD7380DA15B5147DA041549F48E36791C71ED70021D9CD6D8AB15043EF14C16D83DC1C0ECAD90050EB79BC7EA43DE77EB692428EFA669E23A35A8CB2122CF82265"
dec_str = "Hola, Enviamos un código como simulación de transacción para validar y sincronizar su dispositivo."
key_str = bruteforce_key(ciphered_str, dec_str)
print(key_str)
print("".join([chr(x) for x in key_str]))The output will be as follows:
[53, 86, 65, 78, 86, 52, 83, 68, 77, 67, 51, 86, 69, 65, 70, 82, 56, 83, 50, 209, 51, 77, 57, 85, 54, 87, 82, 72, 51, 80, 55, 70, 68, 68, 57, 84, 57, 81, 188, 48, 73, 65, 71, 53, 87, 90, 74, 53, 75, 53, 53, 86, 65, 210, 86, 52, 83, 68, 77, 67, 51, 86, 69, 65, 70, 82, 56, 83, 50, 77, 51, 77, 57, 85, 54, 87, 82, 72, 51, 80, 55, 70, 68, 68, 57, 84, 57, 81, 49, 48, 73, 65, 71, 53, 87, 90, 74, 53]
5VANV4SDMC3VEAFR8S2Ñ3M9U6WRH3P7FDD9T9Q¼0IAG5WZJ5K55VAÒV4SDMC3VEAFR8S2M3M9U6WRH3P7FDD9T9Q10IAG5WZJ5Once we have this decryption key, you can code the decryption function (it is very easy, you just need to adapt a little bit the code of bruteforce_key). For instance:
def decipher(key_str, enc_str):
idx = 0
# first iteration
edi = int(enc_str[idx:idx + 2], base = 16)
idx += 2
deciphered_str = []
key_idx = 0
while True: # is ugly, but it works :)
var2 = int(enc_str[idx: idx + 2], base = 16)
xor_val = key_str[key_idx] ^ var2
sub = xor_val - edi
if (sub < 0): # check if negative
sub += 255
deciphered_str.append(sub)
key_idx += 1
edi = var2
idx += 2
if idx >= len(enc_str):
return deciphered_strAnd then decrypt the strings of the banks provided in the report of INCIBE:
bbvaes
bankiaes
cajamares
caixabankes
bancsabadellcom
unicajabancoes
pibankes
cetelemes
caixaenginyerscom
ingingdirectes
ibercajaes
cecabankes
bankingtriodoses
bancaadistancialibeÞbankes
bancosantanderes
gruposantanderes
bancaelectronicaabaâcacom
laboralkutxacomes
bancomediolanumesesðs
bmedonlinees
bankintercombancaenóome
grupocajaruraleses
bancochilecl
santandercl
bancoestadocl
bancosecuritycl
scotiabankchilecl
bcicl
bancoitaucl
bancobrasilcombr
internetbankingcaixígovbr
bancobradesco
sicoobcombr
sicredicombr
itaucombr
banquepopulairefr
mabanquebnpparibas
caisseepargnefr
creditagricolefr
creditmutuelfr
labanquepostalefr
monespacelclfr
particulierssocieteeneralefr
bankinterpt
novobancopt
indmillenniumbcppt
santanderpt
bancomontepiopt
abancapt
bancobpipt
cgdptAs you can see, there are strings regarding (a large set of) banks of several countries, such as Spain, Chile, Brazil, France, and Portugal. We warn the users of these banks to be suspicious if abnormal behavior is shown when visiting your bank websites (for instance, a closing of the browser window or unusual petitions of credentials).
Indicators of Compromise (IOCs)
You can easily detect if your machine is compromised with this malware by looking at the Registry. The malware makes persistence setting itself in the following Run key:
HKCU\Software\Microsoft\Windows\CurrentVersion\Run\This kind of persistence is widely used by malware, and corresponds to the System persistence mechanisms — Run keys (HKCU root key) category of our proposed taxonomy for ASEPs (which was introduced in our paper “Characteristics and detectability of Windows auto-start extensibility points in memory forensics”).
To work, the malware will create a named pipe that starts with AHK, followed by an arbitrary string of eight chars (apparently, always capital letters). If your system also has any object with this name, it is also an indicative of infection.
And that’s all, folks! In this post we have statically analyzed a piece of x64 assembly code to reverse engineer it, relying on program binary analysis tools such as Ghidra. Other disassembly frameworks, such as radare2, could be also used for this purpose. We then implemented a Python algorithm to get the decryption key, using the insights given by INCIBE, and found the banks affected by this sample of Mekotio. Let me finish this post expressing my gratitude to INCIBE for releasing such an interesting and detailed report of this piece of malware (but please, the next time, do not hide important information for final users!).
